Définition

Enoncé de la loi de Poiseuille

La loi de Poiseuille décrit la varaition de pression d'un Fluide Newtonien réel en Ecoulement stationnaire et Ecoulement stationnaire.
En négligeant l'effet de pesanteur:
$$\Delta P={{\frac{8\eta L}{\pi R^4}D_v}}$$
Avec:

• \(\eta\): Viscosité dynamique
• \(D_v\): Débit volumique
• \(R\): le rayon du guide d'écoulement
• \(L\): la grandeur caractéristique de l'écoulement

:
Démonstration de la loi de Poisueille
1

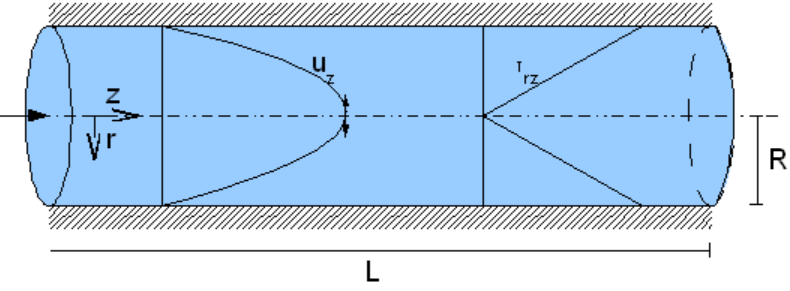
Etude des symétries en coordonnées cylindriques:
$$\implies P(r,\theta, z)=P(r,z)$$
2
Loi de conservation de la masse:
$$div(\vec v)=0$$
$$\vec v=v(r)\vec e_z$$
3
Resolution de l'Equation de Navier-Stokes:
On voit que \(\frac{D\vec v}{Dt}=0\) (Dérivation particulaire)
Alors, en partant de l'hypothèse d'une pesanteur négligée:
$$\vec{grad}(P)=\eta\vec\Delta \vec v$$
4
Finalement:

• \(\frac{\partial P}{\partial r}=0\implies P=P(z)\)
• \(\eta \Delta v(r)=\frac{dP}{dz}\)

$$\eta\Delta v(r)=\frac{dP(z)}{dt}$$
Cette équation n'est vraie en chaque points que si elle est constante:
On pose: \(\frac{dP}{dt}=-K=-\frac{\Delta P}{L}\) (Perte de charge linéique)
5
Il reste à trouver \(v(r)\) qui satisfait \(\eta \Delta v(r)=-K\)
Donc:
$$v(r)=-\frac K\eta \frac {r^2} {4}+c_1\ln(r)+c_2$$
Avec les conditions limites:

• \(r=0\): \(v\) doit être finie donc \(c_1=0\)
• \(r=R\): \(v_{fluide}(R)=v_{conduite}(R)=0\) donc \(c_2=\frac{KR^2}{4\eta}\)

Finalement:
$$v(r)=\frac K\eta \frac {R^2} {4}\left(1-\frac{r^2}{R^2}\right)$$
La vitesse a un profil parabolique comme indiqué sur le schema.
6
On cherche maintenant le Débit volumique:
$$D_v=\iint_S\vec v.d\vec S$$
$$D_v=\frac K\eta \frac {\pi R^4} {8}$$
Or, en regardant l'expression de \(\bar v\), la valeur de moyenne de \(v\):
$$\bar v=\frac 1S\iint_S\vec v.d\vec S$$
On remarque que:
$$D_v=S\bar v$$
7
D'aprés \(D_v=\frac K\eta \frac {\pi R^4} {8}\) et \(K=\frac{\Delta P}{L}\):
On retrouve la loi de Poiseuille:
$$\Delta P=\frac{8\eta L}{\pi R^4}D_v$$